Let the length of the garden be x and the width be y.
It is given that the width of a rectangular garden is 11 feet longer than 3 times its length so it follows:
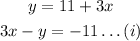
It is also given that the garden's perimeter is 150 feet so it follows:
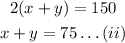
Add equation (i) and (ii) to get:
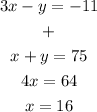
Substitute x=16 in (ii) to get:
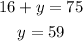
Therefore the dimensions are:
Length=16 feet
Width=59 feet.