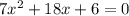Question

how do I do multiplication and division of equations the easiest way, I'm really easily confused and often get distracted.

Answer 1

To explain the multiplication and division of equations, first, we have to define two equations.

`\begin{gathered} 2x+3=3x+1 \\ x=2+5x \end{gathered}`

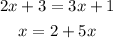
Let's multiply first. To multiply equation, we just have to multiply the left sides and right sides between each other, as follows.

`(2x+3)(x)=(3x+1)(2+5x)`

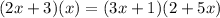
Notice that we are multiplying the left sides and right sides with each other, we are not multiplying the left side of the first equation with the right side of the second equation.

Now, we use the distributive property to solve the products.

`\begin{gathered} 2x\cdot x+3\cdot x=3x\cdot5x+3x\cdot2+1\cdot2+1\cdot5x \\ 2x^2+3x=15x^2+6x+2+5x \end{gathered}`

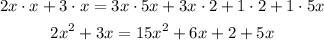
Now, we move all the terms on the right side of equality to the left side.-

`2x^2+3x-15x^2-6x-2-5x=0`

At last. we reduce like terms.

`-13x^2-8x-2=0`

Therefore, the product between the equations is equal to

`-13x^2-8x-2=0`

Now, let's divide the equations we defined at the beginning. We have to divide the left sides and the right sides with each other as we did in the multiplication.

`(2x+3)/(x)=(3x+1)/(2+5x)`

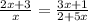
Then, we solve this to express it in its simplest form. First, we multiple in cross way.

`(2x+3)\cdot(2+5x)=(3x+1)\cdot x`

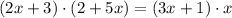
We use the distributive property.

`\begin{gathered} 2x\cdot2+2x\cdot5x+3\cdot2+3\cdot5x=3x\cdot x+1\cdot x \\ 4x+10x^2+6+15x=3x^2+x \end{gathered}`

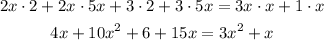
Now, we move all the terms on the right side to the left side of the equality.

`4x+10x^2+6+15x-3x^2-x=0`

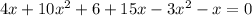
Then, we reduce like terms.

`7x^2+18x+6=0`

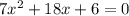
Therefore, the division of the equations would be

`7x^2+18x+6=0`