Answer:
Explanation:
The line is parallel to y = 3x -5, meaning it has the same slope; therefore, we already know that our equation takes the form
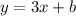
Now, the second requirement is that the line should pass through the point (1, -7), meaning it should satisfy the condition that when x = 1, y = -7. Putting in these values of x and y in the above equation gives
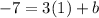

subtracting 3 from both sides gives
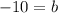
With the value of b in hand, we now have the equation of the line

which is our answer!