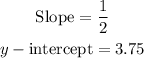Step-by-step explanation:
We are given the following linear equation:
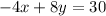
Take note that this is an equation in the STANDARD FORM.
For an equation in the standard form, two main conditions must be satisfied and these are;
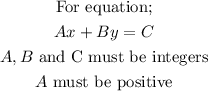
The value of A in our equation is negative. We can now multiply all through by -1, and we'll have;
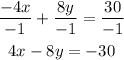
Subtract 4x from both sides;
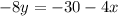
Divide all through by -8;

We can now refine this and re-write in the slope-intercept form;
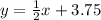
Now take note of the following.
For the equation given in slope-intercept form;


Therefore;
ANSWER: