3u(5u-v)²
STEP - BY - STEP EXPLANATION
What to do?
Factor the given trinomials.
Given:
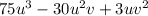
To solve, we will follow the steps below:
Step 1
Factor out 3u from the given trinomials, since 3u is common to all the terms.
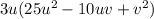
Step 2
Further factorize 25u² - 10uv + v²
Step 3
Find two terms such that its product gives 25u²v² and its sum gives -10uv.
The two terms are -5uv and -5uv.
Step 4
Replace the -10uv by the two terms.
That is;
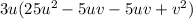
Step 4
Factorize the inner parenthesis.
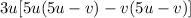
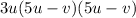
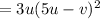
Therefore, the factorized form is 3u(5u-v)²