Hello there. To solve this question, we'll have to remember some properties about rational functions.
Given the functions:
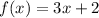
And
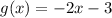
We have to evaluate

For this, remember that:
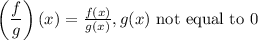
The domain of this function is the entire real line, without the point x such that g(x) = 0.
In this case, we'll have
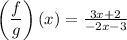
Evaluating it at x = 1, we get
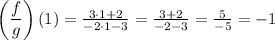
This is the value we've been looking for.