Question

Solve the system using substitution. Show your work! (6 pts)(x = -7y + 32(2x - 2y = 16

Answer 1

The system of equations is:

`\begin{gathered} x=-7y+32 \\ 2x-2y=16 \end{gathered}`

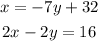
To solve by substitution, first we need to isolate one of the variables. However, this is already done in the first equation.

Next, we want to substitute x into the other equation, so let's do that:

`2(-7y+32)-2y=16`

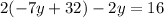
Notice that we divide both sides by two to simplify our work:

`\begin{gathered} (2(-7y+32)-2y)/(2)=(16)/(2) \\ (2(-7y+32))/(2)-(2y)/(2)=(16)/(2) \\ -7y+32-y=8 \end{gathered}`

Now we isolate y:

`\begin{gathered} -7y+32-y=8 \\ -8y+32=8 \\ -8y=8-32 \\ -8y=-24 \\ y=(-24)/(-8)=3 \end{gathered}`

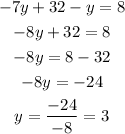
Now that we have y, we substitute in either equations to find x. Let's do it in the first one:

`\begin{gathered} x=-7y+32 \\ x=-7\cdot3+32=-21+32=11 \end{gathered}`

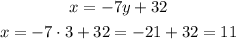
So, y = 3 and x = 11.