Question

A man has 20 coins in his pocket, all of which are dimes and quarters. If the total value of his change is 275cents, how many dimes and how many quarters does he have?Your answer is

Answer 1

From the question, we can say that:

`\begin{gathered} D+Q=20 \\ D*10+Q*25=275 \end{gathered}`

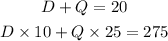
where D stands for the number of dimes and Q for the number of quarters.

If we isolate Q in the first equation/relation we wrote above, and substitute it in the second equation, we will be able to find the number D, as follows:

`\begin{gathered} D+Q=20\to Q=20-D \\ \\ D*10+(20-D)*25=275\to10D+500-25D=275\to \\ \to500-15D=275\to500-275=15D\to15D=225\to D=(225)/(15) \\ \to D=15 \end{gathered}`

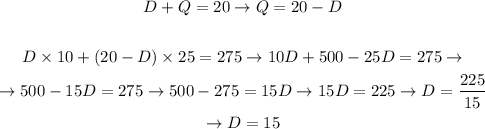
Now, we can substitute the value of D in the first equation, as follows:

`\begin{gathered} D+Q=15+Q=20\to Q=20-15\to \\ \to Q=5 \end{gathered}`

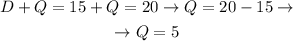
From the present solution, we conclude that the number of dimes equals 15, and the number of quarters is 5.