From the question, we can say that:
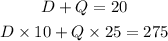
where D stands for the number of dimes and Q for the number of quarters.
If we isolate Q in the first equation/relation we wrote above, and substitute it in the second equation, we will be able to find the number D, as follows:
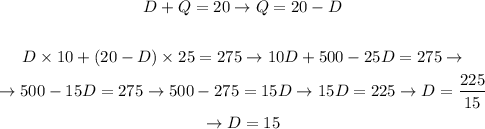
Now, we can substitute the value of D in the first equation, as follows:
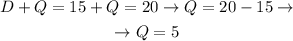
From the present solution, we conclude that the number of dimes equals 15, and the number of quarters is 5.