First, calculate the total number of votes
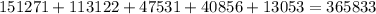
Then, the majority of the votes is
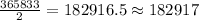
a) At least 182917 votes are needed to get a majority in the Electoral College.
Crawford's votes plus miscellaneous are equal to 53909.
Add them to Jackson's, Adam's, and Clay's to check whether they get a majority that way
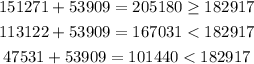
Therefore, only Jackson could have won a majority of the votes.
b)
Calculate the number of extra votes Jackson needs to get a majority
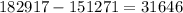
Then, calculate the percentage that 31646 represents if 182917 is 100%.
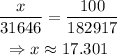
Thus, Jackson needs 17.3% of the votes.