Question

the 1824 presidential election include 4 compatible with Canadian all from democratic Republican Party Android Jackson receive 151271 votes.

Answer 1

First, calculate the total number of votes

`151271+113122+47531+40856+13053=365833`

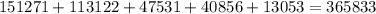
Then, the majority of the votes is

`(365833)/(2)=182916.5\approx182917`

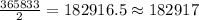
a) At least 182917 votes are needed to get a majority in the Electoral College.

Crawford's votes plus miscellaneous are equal to 53909.

Add them to Jackson's, Adam's, and Clay's to check whether they get a majority that way

`\begin{gathered} 151271+53909=205180\ge182917 \\ 113122+53909=167031<182917 \\ 47531+53909=101440<182917 \end{gathered}`

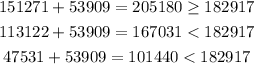
Therefore, only Jackson could have won a majority of the votes.

b)

Calculate the number of extra votes Jackson needs to get a majority

`182917-151271=31646`

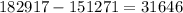
Then, calculate the percentage that 31646 represents if 182917 is 100%.

`\begin{gathered} (x)/(31646)=(100)/(182917) \\ \Rightarrow x\approx17.301 \end{gathered}`

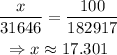
Thus, Jackson needs 17.3% of the votes.