Given the figure of the circle O
As shown, the radius of the circle = r = 9 cm
The measure of the central angle < AOB = 37°
We will find the area of the shaded sector
We will use the following formula:
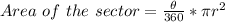
Substitute θ = 37°, and r = 9
So, the area of the sector will be:
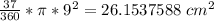
Rounding to the nearest tenth
So, the answer will be: c. 26.2 cm²