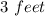Question

The model of an arch is represented by the polynomial function f(x) = -x2 + 6x - 4. f(x) is the height, in feet, of the model from the base. Find the maximum height of the arch model.4 feet5 feet3 feet2 feet

Answer 1

Explanation

We are required to determine the maximum height of the arch model given by:

`f(x)=-x^2+6x-4`

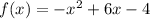
This is achieved thus:

- First, we start by determining the first derivative of the function as follows:

`\begin{gathered} f(x)=-x^2+6x-4 \\ f^(\prime)(x)=-2x+6-0 \\ f^(\prime)(x)=-2x+6 \end{gathered}`

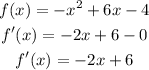
- Next, we equate the derived function to zero and solve for x as follows:

`\begin{gathered} f^(\prime)(x)=-2x+6 \\ \text{ Let }f^(\prime)(x)=0 \\ \therefore-2x+6=0 \\ -2x=-6 \\ (-2x)/(-2)=(-6)/(-2) \\ x=3 \end{gathered}`

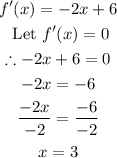
Hence, the answer is:

`3\text{ }feet`