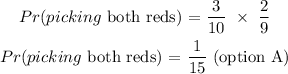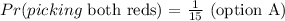
Step-by-step explanation:
number of blue marbles = 2
number of red marbles = 3
number of yellow marbles = 5
Total marbles = 2 + 3 + 5 = 10
Probability of picking both reds = probability of picking red as 1st and red as second
Probability of picking a red marble = number of red marbles/ total marbles
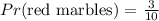
Probability of picking red as 1st = 3/10
For the 2nd picking:
Since it is a probability without replacement (after picking the 1st one, it was not replace), the number of red marbles will reduce by 1
number of red amrbles = 3 - 1 = 2
The total number of marbles will also decrease by 1
Total marbles = 10 - 1 = 9
Probability of picking red as 2nd = 2/9