Question

Can you please help me out with a question

Answer 1

16.7%

Step-by-step explanation:

The number of faces in a die = 6

Multiples of 3, {3,6} = 2

`P(m\text{ultiple of 3)}=(2)/(6)`

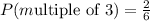
The total number of cards in a standard deck = 52

Number of red cards = 26

`\begin{gathered} P(\text{red card)=}(26)/(52) \\ =(1)/(2) \end{gathered}`

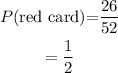
Therefore, the probability that the die will be a multiple of 3 and the card will be red:

`\begin{gathered} =(2)/(6)*(1)/(2) \\ =0.16667 \\ =16.667\% \\ P(mult.\; of\; 3,red\; card)\approx16.7\%\text{ (to the nearest tenth)} \end{gathered}`