Question

Given function f(x) = x - x ^-1/3, find value of x = c that satisfies Roll's Theorem on the interval [0, 1].

Answer 1

- The function given is:

`f(x)=x-x^{-(1)/(3)}`

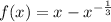
- Rolle's theorem states that:

"if a function f is continuous on the closed interval [a, b] and differentiable on the open interval (a, b) such that f(a) = f(b), then f′(x) = 0 for some x with a ≤ x ≤ b."

- The Rolle's theorem formula is:

`\begin{gathered} f^(\prime)(c)=(f(b)-f(a))/(b-a) \\ where, \\ c\text{ is the value of x that satisfies Rolle's theorem} \end{gathered}`

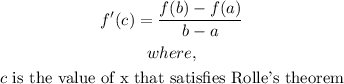
- The interval given to us is [0, 1], this implies that:

`\begin{gathered} a=0 \\ b=1 \end{gathered}`

- We can confirm that:

- Thus, since the values of f(a) and f(b) are not equal, no value of c would satisfy the Rolle's theorem