Look at the graph. You can identify that the Cave entrance is located at this point:

And the Canoe rentals is located at this point:
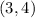
In order to calculate the distance between two points, you can use the following formula:
![d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/be685jmxw05hm2tq94m5iuge2xjynn1hfn.png)
You can set up that:
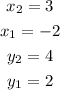
Substitute the corresponding coordinates into the formula and evaluate:
![\begin{gathered} d=\sqrt[]{(3-(-2))^2+(4-2)^2} \\ d=\sqrt[]{29}\text{ units} \\ d=5.38\text{ units} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/j8ko1tqzpnqscq0vjl6kefbtlwq79xwqfs.png)
The distance between the Cave entrance and the Canoe rentals is 5.38 units.