Question

Write this solution in standard form, a + bi, where a and b are real numbers. What are the values of a and b?

Answer 1

Given

`x=\frac{4\pm\sqrt[]{-25}}{4}`

The expression includes the square root of -25. To solve this expression further, you have to use complex numbers.

The unit imaginary number is represented by the letter "i", which is equal to the square root of -1

`i=\sqrt[]{-1}`

You can write the square root of -25 using imaginary numbers as follows:

`\sqrt[]{-25}=\sqrt[]{(-1)\cdot25}=\sqrt[]{-1}\cdot\sqrt[]{25}=i\cdot\sqrt[]{25}`

The square root of 25 is 5 so you can simplify the expression one step more:

`i\sqrt[]{25}=5i`

Now you can write the quadratic equation as follows:

`x=(4\pm5i)/(4)`

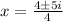
Distribute the division and simplify:

`\begin{gathered} x=(4)/(4)\pm(5i)/(4) \\ x=1\pm(5)/(4)i \end{gathered}`

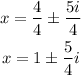
"a" represents the real number, in this case, it is a=1

"b" represents the imaginary part of the number, in this case, b=±5/4

The correct option is the first option.