Given
![x=\frac{4\pm\sqrt[]{-25}}{4}](https://img.qammunity.org/2023/formulas/mathematics/college/m9frj1gi5h3b0wpo62iyyd6tt6z5pz2cce.png)
The expression includes the square root of -25. To solve this expression further, you have to use complex numbers.
The unit imaginary number is represented by the letter "i", which is equal to the square root of -1
![i=\sqrt[]{-1}](https://img.qammunity.org/2023/formulas/mathematics/college/prwnjpkamd054mvqxx3wkz9peqbswm21lz.png)
You can write the square root of -25 using imaginary numbers as follows:
![\sqrt[]{-25}=\sqrt[]{(-1)\cdot25}=\sqrt[]{-1}\cdot\sqrt[]{25}=i\cdot\sqrt[]{25}](https://img.qammunity.org/2023/formulas/mathematics/college/h9sld9pprypgtnnwqb3adaeoemlilb3zvw.png)
The square root of 25 is 5 so you can simplify the expression one step more:
![i\sqrt[]{25}=5i](https://img.qammunity.org/2023/formulas/mathematics/college/tjld2n30fbbplmgsoy9267vgu2ve4uhi2p.png)
Now you can write the quadratic equation as follows:
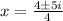
Distribute the division and simplify:
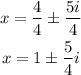
"a" represents the real number, in this case, it is a=1
"b" represents the imaginary part of the number, in this case, b=±5/4
The correct option is the first option.