Question

Consider the radical equation √(x+3)=4. Solve this equation by squaring both sides and then solving for x. Now, replace 4 by -4 and solve for x again. Is the value you found for x still a solution? Explain your reasoning.

Answer 1

Given the radical eqaution

`\sqrt[]{(x+3)}=4`

To find the value of x

Square both sides of the equation

`\mleft\lbrace\sqrt[]{(x+3)}\mright\rbrace^2=(4)^2`

Solve the brackets

`\begin{gathered} x+3=16 \\ \text{Collect like terms} \\ x=16-3=13 \\ x=13 \end{gathered}`

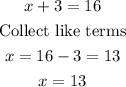
Replacing 4 by -4 in the given radical equation

`\sqrt[]{(x+3)}=-4`

To find the value of x

Square both sides of the equation

`\lbrace\sqrt[]{(x+3)}\rbrace^2=(-4)^2`

Solve the brackets

`\begin{gathered} x+3=16 \\ x=16-3 \\ x=13 \end{gathered}`

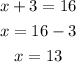
To check:

Substitute 13 for x into both radical equations

For the first equation

`\sqrt[]{(x+3)}=4`

Substituting the value of x into the above equation

`\begin{gathered} x=13 \\ \sqrt[]{(x+3)}=4 \\ \sqrt[]{(13+3)}=4 \\ \sqrt[]{16}=4 \\ 4=4 \end{gathered}`

For the second equation

`\sqrt[]{(x+3)}=-4`

Substituting the value of x into the above equation

`\begin{gathered} \sqrt[]{(x+3)}=-4 \\ \sqrt[]{(13+3)}=-4 \\ \sqrt[]{16}=-4 \\ 4\\e-4 \end{gathered}`

Hence,

`\begin{gathered} x=13\text{ is a solution to }\sqrt[]{(x+3)}=4\text{ (i.e 4 }=4) \\ x=13\text{ is not a solution to }\sqrt[]{(x+3)}=-4\text{ (i.e 4 }\\e-4) \end{gathered}`