Given the radical eqaution
![\sqrt[]{(x+3)}=4](https://img.qammunity.org/2023/formulas/mathematics/college/ocd47nkmzcsqmgcqn9hnp3qsss121gkif7.png)
To find the value of x
Square both sides of the equation
![\mleft\lbrace\sqrt[]{(x+3)}\mright\rbrace^2=(4)^2](https://img.qammunity.org/2023/formulas/mathematics/college/hggjsz6ouxcvzv8kc52ya98h68ab2peuuo.png)
Solve the brackets
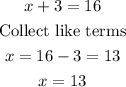
Replacing 4 by -4 in the given radical equation
![\sqrt[]{(x+3)}=-4](https://img.qammunity.org/2023/formulas/mathematics/college/skn1wifhtpnlr843zwm3fxdglvtl13yec9.png)
To find the value of x
Square both sides of the equation
![\lbrace\sqrt[]{(x+3)}\rbrace^2=(-4)^2](https://img.qammunity.org/2023/formulas/mathematics/college/wi7163rwprfc84mdp6c7empo3cythu7c9x.png)
Solve the brackets
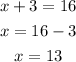
To check:
Substitute 13 for x into both radical equations
For the first equation
![\sqrt[]{(x+3)}=4](https://img.qammunity.org/2023/formulas/mathematics/college/ocd47nkmzcsqmgcqn9hnp3qsss121gkif7.png)
Substituting the value of x into the above equation
![\begin{gathered} x=13 \\ \sqrt[]{(x+3)}=4 \\ \sqrt[]{(13+3)}=4 \\ \sqrt[]{16}=4 \\ 4=4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/7x1m4i21ewj5c83kh8o506g539i94i8c3v.png)
For the second equation
![\sqrt[]{(x+3)}=-4](https://img.qammunity.org/2023/formulas/mathematics/college/skn1wifhtpnlr843zwm3fxdglvtl13yec9.png)
Substituting the value of x into the above equation
![\begin{gathered} \sqrt[]{(x+3)}=-4 \\ \sqrt[]{(13+3)}=-4 \\ \sqrt[]{16}=-4 \\ 4\\e-4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/2oukw4k12273ml74hhxf45ac7kq4qnukqu.png)
Hence,
![\begin{gathered} x=13\text{ is a solution to }\sqrt[]{(x+3)}=4\text{ (i.e 4 }=4) \\ x=13\text{ is not a solution to }\sqrt[]{(x+3)}=-4\text{ (i.e 4 }\\e-4) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/15ye1e0kmpdymra2l0n4h0l5zi1lrdazzf.png)