The given equation of the circle is:
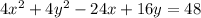
We can start by simplifying this equation by dividing both sides by 4:
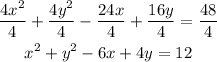
Now, if we subtract 12 from both sides it is written in general form:
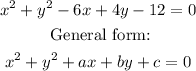
Where a, b and c correspond to:
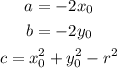
The coordinates of the center of the circle are (x0,y0) and r is the radius.
By replacing the known values we can obtain the center and radius as follows:
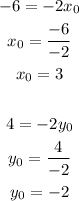
The center of the circle is located at (3,-2).
Let's find the radius:
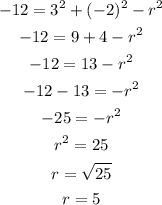
The radius of the circle is 5.
PART B.
By knowing the coordinates of the center and the radius, the graph of the circle looks like this:
PART C.
To find the intercepts, we need to make x=0 and solve for y, and then make y=0 and solve for x as follows:
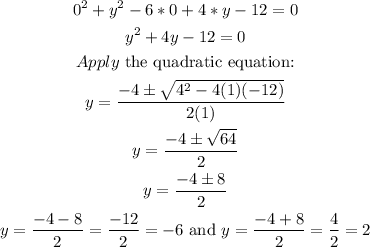
The y-intercepts are y=-6 and y=2.
Now let's find the x-intercepts:

The x-intercepts are x=-1.6 and x=7.6