Question

If cos(t)=\frac{2}{9} and t is in quadrant I then the value of sin(t) is AnswerIf your answer is not an integer then round it to the nearest hundredth.

Answer 1

There is a relation between sine and cosine an angle

`sin^2x+cos^2x=1`

We will use this rule to solve the question

Since cos(t) = 2/9, then substitute it in the rule above

`\begin{gathered} sin^2\left(t\right)+\left((2)/(9)\right)^2=1 \\ sin^2\left(t\right)+(4)/(81)=1 \end{gathered}`

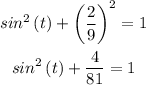
Subtract 4/81 from each side

`\begin{gathered} sin^2\left(t\right)+(4)/(81)-(4)/(81)=1-(4)/(81) \\ sin^2\left(t\right)=(81)/(81)-(4)/(81) \\ sin^2\left(t\right)=(77)/(81) \end{gathered}`

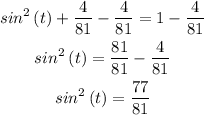
Take a square root for each side

`\begin{gathered} √(sin^2\left(t\right))=\sqrt{(77)/(81)} \\ sin\left(t\right)=(√(77))/(9) \end{gathered}`

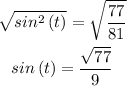
Change it to decimal and round the answer to the nearest hundredth

`sin\left(t\right)=0.97`

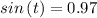
The answer is sin(t) = 0.97