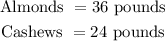Question

Almonds worth $6.00 per pound are to be combined with cashews worth $11.00 per pound to make 60 pounds of a blend worth $8.00 per pound. How many pounds of each type of nut should be used?Almonds: $ poundsCashews: $ pounds

Answer 1

The number of almounds and Cashews used in the blend is;

`\begin{gathered} \text{Almonds }=36\text{ pounds} \\ \text{Cashews }=24\text{ pounds} \end{gathered}`

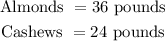
Step-by-step explanation:

Given that Almonds worth $6.00 per pound are to be combined with cashews worth $11.00 per pound to make 60 pounds of a blend worth $8.00 per pound.

Let x and y represent the number of pounds of Almonds and cashews respectively;

The total number of pounds of the blend is;

`x+y=60\text{ -----}1`

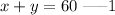
combining with the price;

`\begin{gathered} 6x+11y=60(8) \\ 6x+11y=480\text{ -----}-2 \end{gathered}`

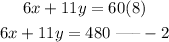
solving the simultaneous equation;

`\begin{gathered} x+y=60\text{ -----}1 \\ 6x+11y=480\text{ -----}-2 \end{gathered}`

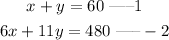
solving by substitution;

`\begin{gathered} \text{from equation 1;} \\ x=60-y \\ \text{substituting into equation 2;} \\ 6x+11y=480 \\ 6(60-y)+11y=480 \\ 360-6y+11y=480 \\ 360+5y=480 \\ 5y=480-360 \\ 5y=120 \\ y=(120)/(5) \\ y=24 \end{gathered}`

Substituting the value of y;

`\begin{gathered} x=60-y \\ x=60-24 \\ x=36 \end{gathered}`

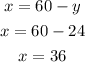
Therefore, the number of almounds and Cashews used in the blend is;

`\begin{gathered} \text{Almonds }=36\text{ pounds} \\ \text{Cashews }=24\text{ pounds} \end{gathered}`