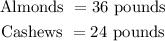Answer:
The number of almounds and Cashews used in the blend is;
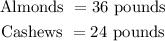
Step-by-step explanation:
Given that Almonds worth $6.00 per pound are to be combined with cashews worth $11.00 per pound to make 60 pounds of a blend worth $8.00 per pound.
Let x and y represent the number of pounds of Almonds and cashews respectively;
The total number of pounds of the blend is;
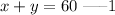
combining with the price;
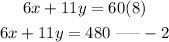
solving the simultaneous equation;

solving by substitution;

Substituting the value of y;
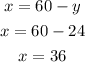
Therefore, the number of almounds and Cashews used in the blend is;