We need to write the vertex form of the quadratic function:
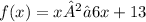
The vertex form of a quadratic function is written as:

where a is the leading coefficient and (h,k) is the vertex of the parabola.
We have:
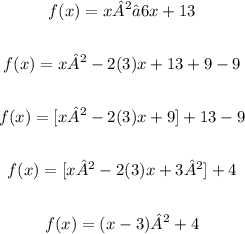
Thus, we obtained:
• a = 1
,
• h = 3
,
• k = 4
Since the leading coefficient is positive, the parabola opens upwards. Therefore, the y-coordinate of its vertex (k) is the minimum value of f(x).
Answer
Vertex form: f(x) = (x - 3)² + 4
Minimum value of f(x): 4