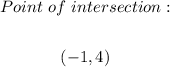Question

Find the point at which the line f(x) = 3x + 7 intersects the line g(x) = - 5x - 1

Answer 1

GIVEN:

We are given the following pair of functions f and g as follows;

`\begin{gathered} f(x)=3x+7 \\ \\ g(x)=-5x-1 \end{gathered}`

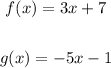
Required;

To find the point at which the line f(x) intersects the line g(x).

Step-by-step solution;

To begin with, take note that the functions f and g can also be expressed in form of an equation.

The output will simply take the form of y and we will have both functions refined as shown below;

`\begin{gathered} y=3x+7-----(1) \\ \\ y=-5x-1-----(2) \end{gathered}`

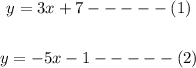
Now we have a system of equations which we can solve using the elimination method.

Subtract equation (2) from (1);

`\begin{gathered} y-y=3x-(-5x)+7-(-1) \\ \\ 0=3x+5x+7+1 \\ \\ 0=8x+8 \\ \\ Subtract\text{ }8\text{ }from\text{ }both\text{ }sides: \\ \\ -8=8x \\ \\ divide\text{ }both\text{ }sides\text{ }by\text{ }8: \\ \\ -1=x \end{gathered}`

Now we have the value of x. We shall substitute this into equation (1) as follows;

`\begin{gathered} y=3x+7 \\ \\ y=3(-1)+7 \\ \\ y=-3+7 \\ \\ y=4 \end{gathered}`

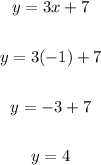
We now have the values of x and y for both equations. This means for functions f and g, the input x = -1 will produce the output f(x) = 4.

ANSWER:

`\begin{gathered} Point\text{ }of\text{ }intersection: \\ \\ (-1,4) \end{gathered}`