Question

The cost function for a certain company is C = 50x + 400 and the revenue is given by R = 100x − 0.5x^2. Recall that profit is revenue minus cost. Set up a quadratic equation and find two values of x (production level) that will create a profit of $400.

Answer 1

The cost and revenue functions are given to be:

`\begin{gathered} C=50x+400 \\ R=100x-0.5x^2 \end{gathered}`

Recall that profit is revenue minus cost. If the profit is $400, we have that:

`R-C=400`

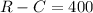
Therefore, we have:

`100x-0.5x^2-50x-400=400`

Rearranging, we have the equation to be:

`-0.5x^2+50x-800=0`

Solving the quadratic equation using the quadratic formula, we have:

`\begin{gathered} x=(-b\pm√(b^2-4ac))/(2a) \\ a=-0.5,b=50,c=-800 \\ \therefore \\ x=(-50\pm√(50^2-2(-0.5*-800)))/(2*-0.5) \end{gathered}`

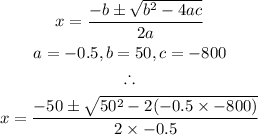
Therefore, we can calculate the values of x to be:

`x=20,x=80`

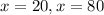
Hence, the two values of x are 20 and 80.