Question

Determine whether figure ABCD is a parallelogram. (let me know if you need to see the drop down options)

Answer 1

Given:

A(1,2)

B(3,4)

C(3,-1)

D(1,-3)

Solution:

We are asked to justify the argument using the slope formula and the distance formula.

Slope Formula:

`m=(y_2-y_1)/(x_2-x_(`1))`

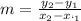
Distance Formula:

`d=\sqrt[]{(x_2_{}-x_1)^2^{}_{}+(y_2-y_1_{})^2}`

Now, we will use the given to find the slope and the distance inorder to answer the questions.

For the slopes:

`\begin{gathered} m_(AB)=(4-2)/(3-1) \\ m_(AB)=(2)/(2) \\ m_(AB)=1 \end{gathered}`

`\begin{gathered} m_(CD)=(-3+1)/(1-3) \\ m_(CD)=(-2)/(-2) \\ m_(CD)=1 \end{gathered}`

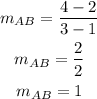
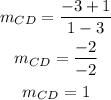
The slopes of AB and CD are equal.

For the distances:

`\begin{gathered} d_(AB)=\sqrt[]{(3_{}-1_{})^2_{}+(4_{}-2_{})^2} \\ d_(AB)=\sqrt[]{2^2+2^2} \\ d_(AB)=\sqrt[]{8} \\ d_(AB)=2\sqrt[]{2} \end{gathered}`
`\begin{gathered} d_(CD)=\sqrt[]{(1_{}-3_{})^2_{}+(-3_{}+1_{})^2} \\ d_(CD)=\sqrt[]{(-2)^2+(-2)^2} \\ d_(CD)=\sqrt[]{8} \\ d_(CD)=2\sqrt[]{2} \end{gathered}`

ANSWER:

Yes, ABCD is a paralellogram.

AB is equal to CD and the slopes of AB and CD are equal, so one pair of opposite sides is both parallel and congruent.