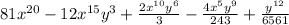SOLUTION
For the expression
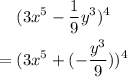
(a) The summation notation that he will use to expand the expression would be
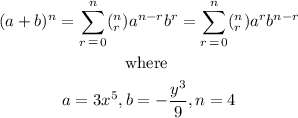
substituting the values of a, b and n, we have
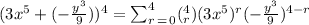
Hence the answer is
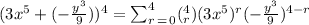
(b) So, expanding we have
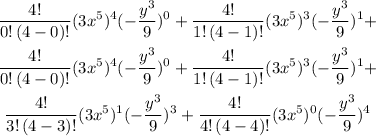
Continuing the expansion we have
Then the final answer becomes