We need to calculate
Horizontal forces sum
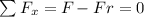
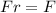
F is the applied force and Fr is the friction force
If F=35.2N, therefore Fr=35.2N
Then for the sum of vertical forces
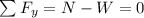
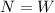
where N is the normal force and W is the weigth
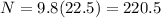
Then for the coefficient, we have
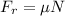
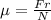
We substitute the values to obtain the coefficient
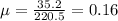
The coefficient of friction is 0.16
Then for the next question
As the angle of inclination increased, the normal force decreased, as we can see in the formula we use previously that will be caused a decrease in the frictional force. Therefore a decrease in the angle of inclination will cause an increase in the friction force.