ANSWER
Step-by-step explanation
We want to solve the given polynomial:
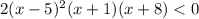
First, let us find the critical points of the polynomial:

Now, we have to test the intervals between the critical points to see which of them will solve the inequality.
CASE 1: x < -8 (Use x = -9)
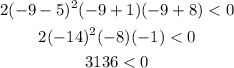
As we can see, this does not work in the original inequality.
CASE 2: -8 < x < -1 (Use x = -6)
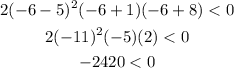
As we can see, this works in the original inequality.
CASE 3: -1 < x < 5 (Use x = 4)
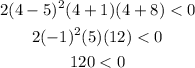
As we can see, this does not work in the original inequality.
CASE 4: x > 5 (Use x = 10)
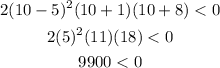
As we can see, this does not work in the original inequality.
Therefore, the solution of the polynomial inequality given is:
[tex]\begin{gathered} -8