Given the equation :
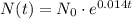
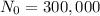
We need to find the number of bacteria after 3 hours
so, t = 3 * 60 = 180 minutes
Substitute with t = 180 at the given equation
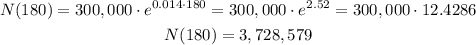
So, after 3 hours , the number of bacteria = 3,728,579
to the nearest thousand it will be : 3,729,000