Answer:
1604.4 sq. cm.
Explanation:
The base of the solid is a regular hexagon.
A regular hexagon can be divided into 6 equilateral triangles.
• Base of one of the triangles, s = 14 cm
,
• Height of one of the triangles, a = 12.1 cm
First, calculate the area of the hexagonal base.
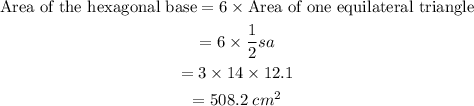
Next, calculate the lateral surface area (area of the sides).
The side of the solid is made up of 6 rectangles with dimensions 7cm by 14cm.
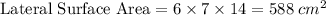
Therefore, the surface area of the solid will be:

The total surface area is 1604.4 sq. cm.