Step-by-step explanation
The three forms of the quadratic equation can be given as
Part A
1) Standard Form
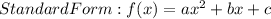
2) Factored form
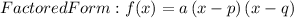
3) Vertex form
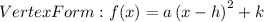
Part B
For the standard form, the vertex is given by
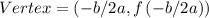
For the factored form, the vertex is given by;
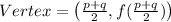
For the vertex form
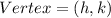
Part C
For the standard form, the axis of symmetry is given by

For the vertex form. the axis of symmetry is given by
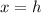
For the factored form, the axis of symmetry is
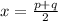
Part C
I prefer the factored form because we can determine end behavior using the value of "a." Although the degree is not as easily identifiable, we know there are only two factors, making the degree two.
Also, we can easily identify the zeros or x-intercepts of the function. This is given by the values of p and q.
Lastly, we can easily get the vertex using the formula denoted above.
Only the factored form easily offers the three possiblities written above.