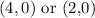The Solution:
Given the function:
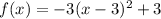
We are asked to find the y-intercepts of the above function.
Recall:
x-intercepts of a function are the values of x for which the function is zero. That is if y=f(x) then the x-intercept is the value of x when y=f(x)=0
Similarly,
y-intercepts of a function are the values of y for which x is zero.
So, in this case, the y-intercept is:
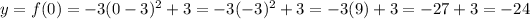
So, the y-intercept is:
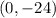
To find the x-intercept:
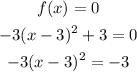
Dividing both sides by -3, we get

Taking the square root of both sides, we get
![\begin{gathered} x-3=\text{ }\sqrt[]{1} \\ x-3=\pm1 \\ x=3\pm1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/l1ngxp7moio21gwbndiaoc72mi5i416pxz.png)
This means:
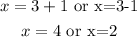
So, the x-intercepts are: