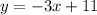Given a line l, if the following points
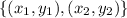
belongs to the line l, the slope m of this line is given by the following formula

Using this formula in our problem, we have
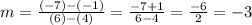
The slope of our line is - 3.
The slope intercept form is

where m represents the slope and b the y-intercept.
We already calculated the slope, if we substitute its value on this form and evaluate one of the points, we can solve the equation for b.

Our line equation is