Question

Use the appropriate amortization formula to find (a) the monthly (n=12) payment on a loan with the given conditions and (b) the total interest that will be paid during the term of the loan.$8,400 is amortized over 9 years at an interest rate of 9.9%

Answer 1

a) In order to calculate the monthly payment for the amortization, we can use the formula:

`A=P(i(1+i)^n)/((1+i)^n-1)`

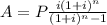
Where A is the periodic payment amount, P is the principal amount, i is the interest rate and n is the total number of payments.

Since we have monthly payments, we can multiply the value of n (initially we have n = 9) by 12 and divide the interest rate by 12, so we have:

`\begin{gathered} A=8400((0.099)/(12)(1+(0.099)/(12))^(9\cdot12))/((1+(0.099)/(12))^(9\cdot12)-1) \\ A=8400(0.00825\cdot2.42867)/(2.42867-1) \\ A=117.81 \end{gathered}`

So the monthly payment is $117.81.

b) First let's calculate the total value paid:

`A\cdot(12n)=117.81\cdot108=12723.48`

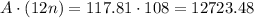
Now, subtracting from the principal, we have the interest:

`I=12723.48-8400=4323.48`

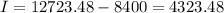
So the total interest is $4323.48.