Question

The functions fand g are shown below.f(x) = 5 - 4Which of the following statements is true?

Answer 1

Let us calculate the y-intercepts and average rate of change over the given intervals.

Function F

`f(x)=5^x-4`

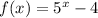
The y-intercept is gotten at x = 0:

`\begin{gathered} f(0)=5^0-4=1-4 \\ f(0)=-3 \end{gathered}`

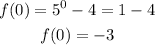
The average rate of change can be calculated using the formula:

`m=(f(b)-f(a))/(b-a)`

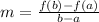
Using [0, 2] as [a, b], we have:

`\begin{gathered} f(0)=-3 \\ f(2)=5^2-4=25-4=21 \end{gathered}`

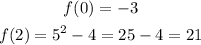
Therefore, we can solve to give:

`\begin{gathered} m_f=(21-(-3))/(2-0)=(24)/(2) \\ m_f=12 \end{gathered}`

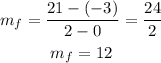
Function G

The graph is given in the question.

The y-intercept is approximately -3.

The average rate of change can be calculated using the following parameters;

`\begin{gathered} f(a)=-3 \\ f(b)=13 \end{gathered}`

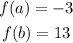
Therefore, we can solve to give:

`\begin{gathered} m_g=(13-(-3))/(2-0)=(16)/(2) \\ m_g=8 \end{gathered}`

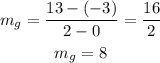
CONCLUSION

The two graphs have the same y-intercept.

The average rate of change in graph g is less than f.

The correct option is OPTION B.