Answer:
(a) x is a variable, t is a constant
(b)t=-2/5
Explanation:
Given f(x) defined below:
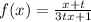
Part A
The value of x can take on any value, which means, it varies.
• Thus, x is a variable.
Since the function, f(x) is a function of x, t is a constant.
Part B
If f(3)=-1
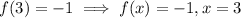
Substitute into f(x) above.
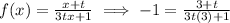
Cross multiply
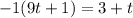
Distribute the bracket on the left-side.
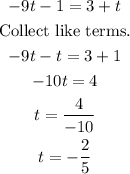
The value of t when f(3)=-1 is -2/5.