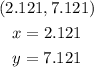The Solution:
The equation for a circle with center ( h , k ) and radius r is:
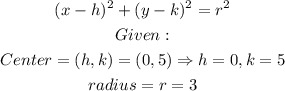
Required:
To find the point in the first quadrant, where the line y = x + 5 intersects the given circle.
Step 1:
Write out the equation of the circle and that of the line.
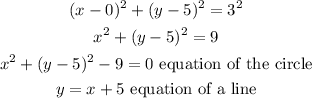
Plotting the graphs of both equations, we have:
Therefore, the correct answer is: