Question

X is the midpoint of line segment WZ. Y is the midpoint of line segment XZ. W is located at (12, 8) and Z is at (0, -4). What are the coordinates of Y?

Answer 1

The diagram above shows Y is the midpoint of line XZ while X is the midpoint of line WZ,

Formula to find the midpoint of a line is given below as,

`\text{Midpoint of a line = (}(x_1+x_2)/(2)),((y_1+y_2)/(2))`

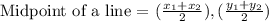
Where the coordinates of points W and Z are,

`\begin{gathered} W(x_(1,)y_1)=(12,8) \\ Z(x_2,y_2)=(0,\text{ -4)} \end{gathered}`

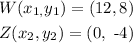
Substituting (x, y) coordinates to find the midpoint, X of line WZ,

`\begin{gathered} X=((12+0)/(2)),((8+(-4))/(2))=((12)/(2),(8-4)/(2))=(6,(4)/(2))=(6,2) \\ \text{Hence, the coordinates of X are (6, 2)} \end{gathered}`

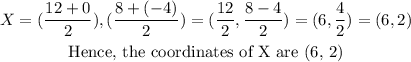
Recall, Y is the midpoint of XZ,

Where the coordinates of points X and Z are,

`\begin{gathered} X(x_1,y_1)=(6,2)_{} \\ Z(x_2,y_2)=(0,-4) \end{gathered}`

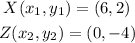
Substituting (x, y) coordinates to find the midpoint, Y of line XZ,

`\begin{gathered} Y=((6+0)/(2)),((2+(-4))/(2))=((6)/(2)),((2-4)/(2))=(3,(-2)/(2))=(3,-1) \\ \text{Hence, the coordinates of Y are (3, -1)} \end{gathered}`

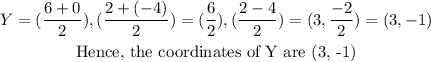
The coordinates of point Y are (3, -1).