Question

A positive integer is 5 less than another. If the sum of the reciprocal of the smaller andtwice the reciprocal of the larger is 11/14, find the two integers

Answer 1

Given that a positive interger is 5 less than another integer, we have the equation:

a = b - 5

Where a represents the smaller interger and b represents the larger interger.

Also, the sum of the reciprocal of the smaller interger and twice the reciprocal of the larger is 11/14. we have the equation:

`(1)/(a)+(2*(1)/(b))=(11)/(14)`

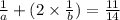
Thus, we have the system of equations:

`\begin{gathered} a=b-5 \\ \\ (1)/(a)+(2)/(b)=(11)/(14) \end{gathered}`

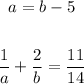
Let's solve for a and b simultaneously using substitution method.

Susbtitue (b - 5) for a in equation 2:

`(1)/(b-5)+(2)/(b)=(11)/(14)`

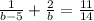
Solving further:

`\begin{gathered} (1)/(b-5)+(2)/(b)=(11)/(14) \\ \\ (b+2(b-5))/(b(b-5))=(11)/(14) \\ \\ (b+2b-10)/(b(b-5))=(11)/(14) \\ \\ (3b-10)/(b(b-5))=(11)/(14) \end{gathered}`

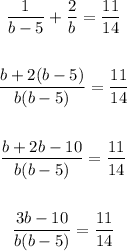
Cross multiply:

`\begin{gathered} 14(3b\text{ -10) = 11(b(b-5))} \\ \\ 42b-140=11(b^2-5b) \\ \\ 42b-140=11b^2-55b \\ \\ -140=11b^2-55b-42b \\ \\ 11b^2-55b-42b=-140 \\ \\ 11b^2-97b=-140 \end{gathered}`

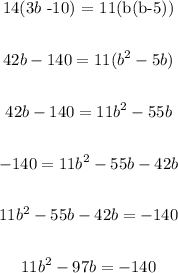
Equate to zero:

`11b^2-97b+140=0`

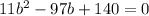
Factor the equation by grouping:

`\begin{gathered} 11b^2-20b-77b+140=0 \\ \\ b(11b-20)-7(11b-20)=0 \\ \\ We\text{ have:} \\ (b-7)(11b-20) \end{gathered}`

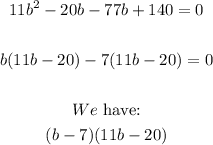
Equate each factor to zero and solve for b:

`\begin{gathered} b-7=0 \\ \\ \text{ b=7} \end{gathered}`
`\begin{gathered} 11b-20=0 \\ \\ 11b=0+20 \\ \\ 11b=20 \\ \\ b=(20)/(11) \end{gathered}`

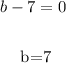
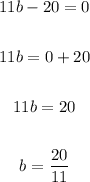
We have the possible values for:

`b=7,\text{ }(20)/(11)`

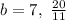
Substitute 7 and 20/11 for b in equation 1 to find a:

`\begin{gathered} a=b-5 \\ \\ a=7-5 \\ \\ a=2 \end{gathered}`
`\begin{gathered} a=b-5 \\ \\ a=(20)/(11)-5 \\ \\ a=-(35)/(11) \end{gathered}`

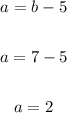
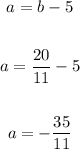
Thus, we have:

`\begin{gathered} \text{When a = 2, b = }7 \\ \\ \text{When a = -}(35)/(11),b=(20)/(11) \end{gathered}`

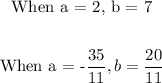
We are told the value of a is a positive integer, let's take the positive values.

Thus, we have:

a = 2, b = 7

The larger interger is 7, while the smaller interger is 2

ANSWER:

Larger interger = 7

Smaller interger = 2