Given that a positive interger is 5 less than another integer, we have the equation:
a = b - 5
Where a represents the smaller interger and b represents the larger interger.
Also, the sum of the reciprocal of the smaller interger and twice the reciprocal of the larger is 11/14. we have the equation:
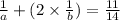
Thus, we have the system of equations:
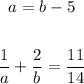
Let's solve for a and b simultaneously using substitution method.
Susbtitue (b - 5) for a in equation 2:
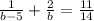
Solving further:
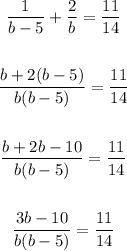
Cross multiply:
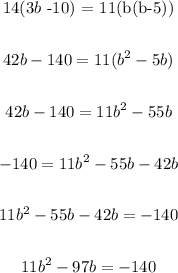
Equate to zero:
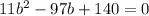
Factor the equation by grouping:
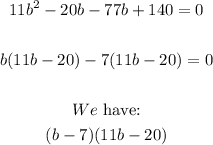
Equate each factor to zero and solve for b:
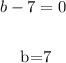
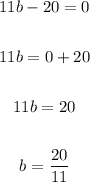
We have the possible values for:
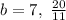
Substitute 7 and 20/11 for b in equation 1 to find a:
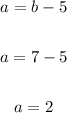
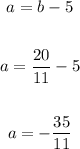
Thus, we have:
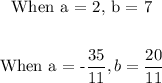
We are told the value of a is a positive integer, let's take the positive values.
Thus, we have:
a = 2, b = 7
The larger interger is 7, while the smaller interger is 2
ANSWER:
Larger interger = 7
Smaller interger = 2