Given
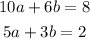
We are to Solve by substitution or elimination.
Solution
Using Elimination method
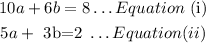
Multiply the second equation by -2, then add the equations together.
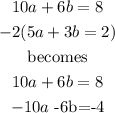
Add these equations to eliminate a:
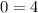
So the answer
No solutions.
Why it is no solution
A system has no solutions if two equations are parallel. ... When two equations have the same slope but different y-axis, they are parallel. Since there are no intersection points, the system has no solutions.