Step 1. Using the first two balances, we can form two equations that will help us to solve the problem.
Let x represent the cubes, y represent the spheres, and z represent the cylinders.
Then, the two equations are:
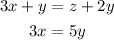
Step 2. We can simplify the first equation by substituting the second equation into it:

And now we simplify the operations between like terms in this last equation:
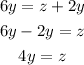
Step 3. So far, we have two equations that relate the x, y, and z values:
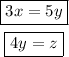
Step 4. In question #3 we are given a value for the sphere (remember that for us the sphere is y), and that value is 9 pounds:
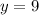
To find the weight of the cube and the cylinder (x and z) we substitute the given value of y into our two equations from step 3:

Solving the first equation for x and the second for z:

The cube weighs 15 pounds and the cylinder weighs 36 pounds.
Answer: 15 and 36