How would i answer and what would be the answer?

Question

asked Dec 7, 2023 194k views

1 Answer

EyalS · Answer 1 · 2023-12-12T02:23:12+0000

Given:

We need to find asymptotes of the given function.

Recall that a horizontal asymptote is a horizontal line, y=a, that has the property that either:

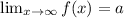
$\lim _(x\to\infty)f(x)=a$

or

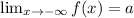
$\lim _(x\to-\infty)f(x)=a$

Taking the limit of the given function, we get

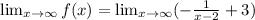
$\lim _(x\to\infty)f(x)=\lim _(x\to\infty)(-(1)/(x-2)+3)$

$\lim _(x\to\infty)f(x)=0+3$

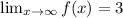
$\lim _(x\to\infty)f(x)=3$

The horizontal asymptote is y=3.

Recall that a vertical asymptote is a vertical line, x=a, that has the property that either:

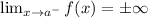
$\lim _(x\to a^-)f(x)=\pm\infty$

or

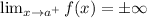
$\lim _(x\to a^+)f(x)=\pm\infty$

Taking limit to the given function, we get

$\lim _(x\to a^+)f(x)=\lim _(x\to a^+)(-(1)/(x-2)+3)$

If we take a=2, the limit will be infinity.

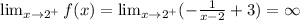
$\lim _(x\to2^+)f(x)=\lim _(x\to2^+)(-(1)/(x-2)+3)=\infty$

Hence the vertical asymptotes x=2.

From these two asymptotes, we can say that the first option or third option would be the graph.

Consider the point (3,2) from the first option graph.

Substitute x=3 and f(3)=2 in the given function, we get

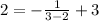
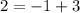
The point (3,2) satisfies the given function.

Hence the graph of the function is