Given:
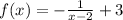
We need to find asymptotes of the given function.
Recall that a horizontal asymptote is a horizontal line, y=a, that has the property that either:
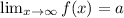
or
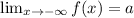
Taking the limit of the given function, we get
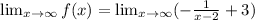
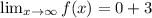
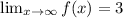
The horizontal asymptote is y=3.
Recall that a vertical asymptote is a vertical line, x=a, that has the property that either:
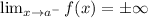
or
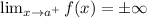
Taking limit to the given function, we get
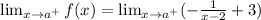
If we take a=2, the limit will be infinity.
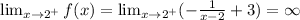
Hence the vertical asymptotes x=2.
From these two asymptotes, we can say that the first option or third option would be the graph.
Consider the point (3,2) from the first option graph.
Substitute x=3 and f(3)=2 in the given function, we get
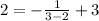
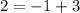
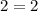
The point (3,2) satisfies the given function.
Hence the graph of the function is