Answer:
• 3y+x=13
,
• y+3x=7
,
• y-x=3
Step-by-step explanation:
Given points A(4,3), B(0,7), C(-1,2):
First, we find the coordinates of the midpoints of AB, AC and BC.
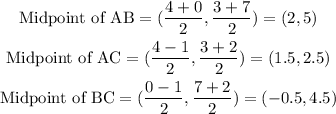
Part 1
The equation of the median from A to BC.
Using points: A(4,3) and (-0.5,4.5) in the two-point form, we have:
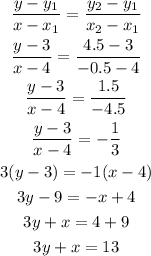
Part 2
The equation of the median from B to AC.
Using points: B(0,7) and (1.5,2.5) in the two-point form, we have:

Part 3
The equation of the median from C to AB.
Using points: C(-1,2) and (2,5) in the two-point form, we have:
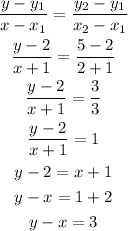
The equations of the medians are:
• 3y+x=13
,
• y+3x=7
,
• y-x=3