Question

Use the two-point form to find the equation of each median of AABC. (Recall that a median of a triangle is the line drawn from any vertex to the midpoint of the opposite side.)A(4,3), B(0,7), C(-1,2)Find the equation of each altitude of AABC. (Recall that an altitude of a triangle is the perpendicular drawn from any vertex to the opposite side.) A(4,3), B(0,7), C(-1,2)

Answer 1

• 3y+x=13

,

• y+3x=7

,

• y-x=3

Step-by-step explanation:

Given points A(4,3), B(0,7), C(-1,2):

First, we find the coordinates of the midpoints of AB, AC and BC.

`\begin{gathered} \text{Midpoint of AB}=\mleft((4+0)/(2),(3+7)/(2)\mright)=(2,5) \\ \text{Midpoint of AC}=\mleft((4-1)/(2),(3+2)/(2)\mright)=(1.5,2.5) \\ \text{Midpoint of BC}=\mleft((0-1)/(2),(7+2)/(2)\mright)=(-0.5,4.5) \end{gathered}`

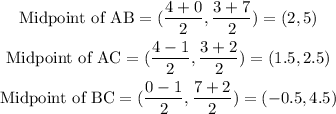
Part 1

The equation of the median from A to BC.

Using points: A(4,3) and (-0.5,4.5) in the two-point form, we have:

`\begin{gathered} (y-y_1)/(x-x_1)=(y_2-y_1)/(x_2-x_1) \\ (y-3)/(x-4)=(4.5-3)/(-0.5-4) \\ (y-3)/(x-4)=(1.5)/(-4.5) \\ (y-3)/(x-4)=-(1)/(3) \\ 3(y-3)=-1(x-4) \\ 3y-9=-x+4 \\ 3y+x=4+9 \\ 3y+x=13 \end{gathered}`

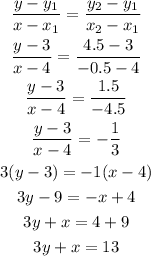
Part 2

The equation of the median from B to AC.

Using points: B(0,7) and (1.5,2.5) in the two-point form, we have:

`\begin{gathered} (y-y_1)/(x-x_1)=(y_2-y_1)/(x_2-x_1) \\ (y-7)/(x-0)=(2.5-7)/(1.5-0) \\ (y-7)/(x)=(-4.5)/(1.5) \\ (y-7)/(x)=-3 \\ y-7=-3x \\ y+3x=7 \end{gathered}`

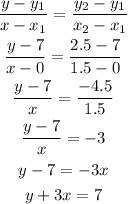
Part 3

The equation of the median from C to AB.

Using points: C(-1,2) and (2,5) in the two-point form, we have:

`\begin{gathered} (y-y_1)/(x-x_1)=(y_2-y_1)/(x_2-x_1) \\ (y-2)/(x+1)=(5-2)/(2+1) \\ (y-2)/(x+1)=(3)/(3) \\ (y-2)/(x+1)=1 \\ y-2=x+1 \\ y-x=1+2 \\ y-x=3 \end{gathered}`

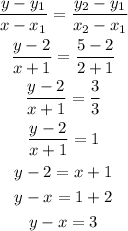
The equations of the medians are:

• 3y+x=13

,

• y+3x=7

,

• y-x=3